Solar wind

Solar wind

by Paul Andrew Cloutier

, 1976.

s:Solar-wind interaction with planetary ionospheres

 

111

SOLAR-WIND INTERACTION WITH PLANETARY IONOSPHERES

P. A. Cloutier

Department of Space Physics and Astronomy
Rice University
Houston, Texas

INTRODUCTION

Planetary encounters by numerous spacecraft launched by the USA and USSR have furnished information concerning the solar-wind interaction with the planets Mercury, Venus, Mars, and Jupiter.  While direct measurements have indicated a wide range of atmospheric densities and intrinsic magnetic field strengths, the data seem to indicate that the flow pattern around nonmagnetized or weakly-magnetized planets with atmospheres optically thick at ionizing wavelengths (that is, with well-developed ionospheres above the planetary surface) is basically the same as that around a strongly-magnetized planet's magnetosphere, such as the Earth's.  The planetary ionosphere apparently presents a hard obstacle to the flow, with bow—shock formation required in the supersonic, super—Alfvénic flow to slow and direct most of the solar—wind plasma around the planetary ionosphere.  In this paper, various aspects of the interaction are examined in the context of theoretical models in an attempt to explain observed details of the interaction regions of Venus and Mars.

NATURE OF THE OBSTACLE—MECHANICS AND ELECTRODYNAMICS

In order to understand the nature of the obstacle presented to the flow by a planetary ionosphere and to be able to predict the details in the flow field around the planet, two basic boundary conditions must be considered. The first condition specifies the behavior of the magnetic field at the lower boundary of the planetary ionosphere, and the second specifies the penetrating solar-plasma flux into a defined upper boundary (ionopause) of the planetary ionosphere. As will be shown, determination of these conditions allows estimation of the parameters of the flow around the planet and of the dynamic behavior of the planetary ionosphere.

The first condition is that, in the absence of an intrinsic planetary magnetic field, the interplanetary magnetic field must become vanishingly small in the lower atmosphere below the ionosphere. This may be simply understood in terms of magnetic diffusion through the highly-conducting dayside ionosphere. The solar-wind flow around the sides of the planet outside the atmosphere carries interplanetary field lines back at a higher rate than the flow through the ionosphere can carry these same field lines (Dessler, 1968). The result is retardation of flux tubes in the ionosphere, with a given flux tube reaching the bottom of the ionosphere behind the segments of the same flux tube carried by the flow around the ionosphere.

112The tension of the field lines will result in rapid straightening and high velocity of the field lines ($v\cong c$) through the neutral atmosphere and planetary body, with very low magnetic flux density there ($B\cong 0$).

The second condition, predicted by theoretical calculations and supported by observational data, is that the planetary ionosphere is nearly impenetrable to the solar-wind plasma. Cloutier et al. (1969) have shown that simultaneous conservation of mass, momentum, and energy in a gas flowing through a region in which cold gas particles are being created (equivalent to planetary photoions being added to the solar wind) is only possible for gas addition rates below a certain critical value. Above this critical value, the flow can no longer accommodate the added mass by adjustment of its velocity, pressure, and density, and a disturbance must propagate upstream to alter the incident flow. Calculations in a one-dimensional model with realistic photoionization rates and solar-wind parameters have placed an upper limit of 1 km/s on the penetration velocity of the solar wind into the atmosphere. This in turn requires bow-shock formation in the solar wind, with less than one percent of the incident flow actually penetrating into the atmosphere, and most of the flow being directed around the planet in the post-shock region (Michel, 1971). The flow field around the planet may therefore be described to an excellent approximation by the aerodynamic models of Spreiter et al. (1966, 1968, 1970) with an impenetrable boundary surface between the solar wind and the ionosphere. A qualitative model of the flow region is shown in figure 1.

The combination of the two boundary conditions described above also allows calculation of the flow field within the ionosphere and of the electric and magnetic field configuration there. From the first boundary condition, the total ionospheric current magnitude required to reduce the shock-compressed interplanetary field to zero at the base of the ionosphere can be estimated. For an interplanetary field of $5\gamma$ , the height-integrated current magnitude is roughly 3 × 1O^-2 amps/m length along the equator (Cloutier and Daniell, 1973). Using model atmospheres for Venus and Mars to calculate the tensor conductivity profiles within the atmosphere, and using the dynamo $v\times B$ electric field from Spreiter's models, it is possible to estimate the subsolar height of the ionopause boundaries for these planets at which the cancellation currents are obtained. These height ranges are shown for Venus in figure 2 and for Mars in figure 3. The effects of any intrinsic magnetic field on Mars are omitted to demonstrate the effects of the purely ionospheric obstacle. The higher apparent obstacle height reported by Gringauz et al. (1975) at Mars may be due to the effects of an intrinsic Martian dipole reported by Dolginov et al. (1973). The height of the obstacle and of the shock will be discussed in greater detail in a later section.

The volume distribution of currents within the ionospheres may be determined by minimization of the volume integral of Joule heating by a variational technique. Recent calculations for Venus have indicated a total potential difference between polar terminators at the 113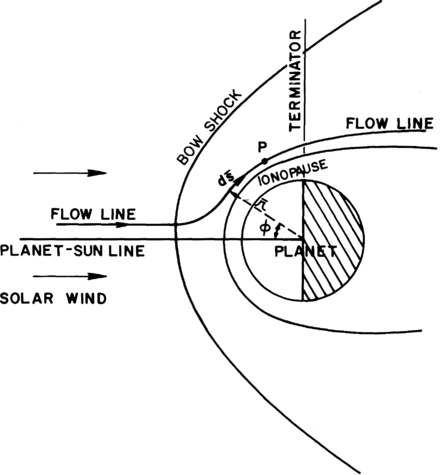

Figure 1. Plasma flow geometry in the vicinity of a nonmagnetic planet.

ionopause boundary of roughly 40 V. This corresponds to less than 0.1 percent of the solar-wind plasma incident on the planet penetrating the ionopause. The volume current distribution together with the conductivity allows determination of electric and magnetic fields everywhere within the ionosphere, and hence specifies the convection pattern of ionization within the ionosphere. A quantitative understanding of the distribution of ionization must clearly include these convective effects with diffusive and photochemical mechanisms.

114

Figure 2. Total ionospheric current magnitude induced in the Venusian ionosphere by the solar wind. The vertical dashed line indicates the current magnitude required to cancel the shock-compressed interplanetary magnetic field. The various curves shown are labelled with ratio H/r0 of scale height to planetary radius and the percentage of He upper limit corresponding to 10⁷ cm^-3 at 200 km altitude. Above 300 km H/r0 should be 0.06 Standoff altitudes are given at subsolar point.

Figure 3. Total ionospheric current magnitude induced in the Martian ionosphere by the solar wind. H/r0 ≈ 0.01 is appropriate for O⁺, which is expected to be the dominant topside ion.

115

SHAPE OF THE OBSTACLE—SYMMETRIES AND ASYMMETRIES

Although the flow patterns calculated by Spreiter et al. (1966, 1968, 1970) are axisymmetric, there are clearly asymmetries between opposite (polar) hemispheres in the altitude distribution of planetary ions added to the flow external to the ionopause owing to the oppositely-directed electric fields as seen from the planetary atmosphere. Cloutier et al. (1974) have considered this effect and concluded that characteristically-different ion densities and energy spectra would be detectable in the two hemispheres. In the hemisphere in which the induced electric field is outward, the ion distribution of a given species is nearly constant between the ionopause and a height of two gyroradii above the ionopause, and decreases exponentially above two gyroradii with roughly the species neutral scale height. In this hemisphere, all ions are accelerated to the average flow velocity. In the opposite hemisphere, in which the electric field is directed inward, the ion distributions are concentrated much closer to the ionopause surface and fall off rapidly with height above it. In this hemisphere, the average drift velocity of ions is less than the flow velocity within two gyroradii of the ionosphere, and varies from ~O at the boundary to the flow velocity at a height of two gyroradii. If the ionopause altitudes in both hemispheres were equal, resulting in equal total mass addition to the flow in the two hemispheres, then clearly the density and velocity differences will result in a difference in momentum transfer from the flow to the photoions. The drag to the flow will be less in the hemisphere in which the electric field is directed inward, and the flow pattern symmetry axis should shift toward this hemisphere. Calculations of the total drag for equal and symmetric ionopause altitudes in both hemispheres show that the altitude of equal drag differs by 300 km at the polar terminators of Venus and 1000 km at the polar terminators of Mars. However, the drag may be equalized by changing the ionopause altitudes slightly to increase the total mass added in one hemisphere and decrease it in the other. The required height differences between hemispheres at the polar terminators are 140 km for Venus and 25 km for Mars, with comparable height differences expected in the shock altitudes.

Another asymmetry may be produced by a combination of two effects. This asymmetry corresponds to a larger effective obstacle polar diameter than equatorial diameter. One contributing effect is the loss in efficiency in the acceleration of planetary photoions by the flow at low (equatorial) latitudes due to decreasing angle between v and B. At the equator, the angle between v and B is very small, and the v X B electric field is much less than at the poles. If the shock-compressed interplanetary field is relatively free of significant fluctuations transverse to the average B, then at low latitudes the momentum transfer from the flow to the planetary photoions, and hence the drag on the flow, will be much less than at the poles. It may be argued, however, that the interplanetary field is not completely noise-free. Measurements in the Earth's magnetosheath indicate an average transverse noise component of 116order 10^-1 of the steady field. Acceleration of planetary photoions at low latitudes may occur in this case by a magnetic pumping mechanism (Alfvén and Falthammar, 1973), with the average ion velocity approaching the flow velocity $v_{0}$ according to the relation:

$v=v_{0}(1-e^{t/T})$

where t is the average time from creation of an ion in the flow, and $\tau$ is the characteristic acceleration time given by:

$\tau \cong (\Delta B/B)^{-2}T_{eye}$

with $\Delta B$ the average transverse field noise component, B the average field magnitude, and $T_{eye}=2\pi m/eB$ the cyclotron period of the ion species of mass, m. Calculation of the resulting average ion velocities at the equatorial terminator for He⁺ on Venus and O⁺ on Mars indicate that these ions have only been accelerated to a few percent of the flow velocity as they cross the terminator. Reduction of ionopause heights at the equator to achieve equality in equatorial and polar drag factors requires a reduction in effective equatorial obstacle radius relative to polar obstacle radius of 650 km for Venus and 250 km for Mars. In addition to this possible asymmetry in the ionopause height from pole to equator, there may be a difference in the height of the shock above the polar and equatorial ionopause boundaries caused by a difference in plasma compressibility. For flow around the ionopause in the equatorial plane, the steady field is nearly parallel to the flow velocity, and the compression and expansion of the plasma along the streamlines is not strongly affected by the magnetic field. Moreover, any transverse magnetic noise component will tend to isotropize the pressure, and instabilities in the flow with $v\|B$ will enhance this effect. The gas in this case should act as an ideal gas with ratio of specific heats $\gamma$ = 5/3. However, for flow over the poles, the streamlines are nearly orthogonal to the magnetic field along the flow tube, and compression and expansion of the plasma involves the magnetic pressure directly. In this case, the ratio $\gamma$ may be closer to 2. This difference in compressibility will cause a significant asymmetry in the shock altitudes from pole to equator even for a completely symmetry ionopause, and the ionopause height asymmetry described above will add to the total shock asymmetry.

The shock positions corresponding to several different Mach numbers for $\gamma$ = 5/3 and 2 have been calculated by Spreiter et al. (1966) for the Earth's magnetosphere, and are shown in figure 4. Direct scaling of this figure to Mars and Venus without inclusion of the ionopause height asymmetries shows that the shock distances at the terminator could differ from pole to equatorial terminator by 1000 km for Mars and 1500 km for Venus due to the compressibility effect alone. The subsolar shock distances extrapolated from the terminator shock distances could differ by 500 km for Mars and 750 km for Venus, leading to obstacle height estimates differing by 350 km for Mars and 500 km for Venus.

117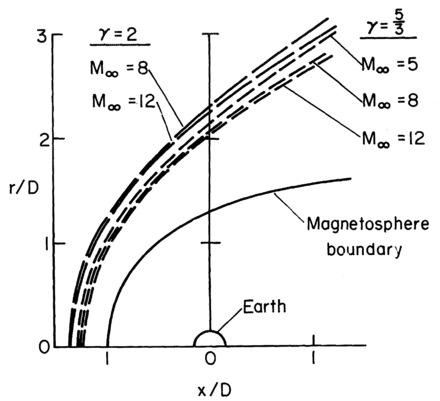

Figure 4. Differences in bow-shock position for $\gamma =5/3$ and $\gamma =2$. The magnetospheric boundary should be scaled to the planetary ionopause surface (from Spreiter et al., 1966).

DISCUSSION

This paper has reviewed a theoretical model for the obstacle presented by a planetary ionosphere to the solar wind. Basic features of this model include small flux penetration of the ionosphere by the solar wind and a weak magnetic field below the dayside ionosphere. The model also predicts that large asymmetries may be found in the ionopause height and shock height from pole to equatorial terminator. The variations in shock height due to these asymmetries are comparable to the variations reported by Gringauz et al. (1974) for Mars, although the variability could also be explained in terms of an asymmetric rotating planetary dipole 118such as that reported by Dolginov et al. (1973). However, for the dipole moment reported of 2.6 X 10²² G cm³, the atmospheric asymmetries may still dominate any effects due to the dipole rotation and control the dynamics of shock formation (Rassbach et al., 1974).

The reported observation of constant magnetic field direction within the Martian nightside obstacle boundary offers a stronger argument in support of an intrinsic Martian field than the observations of shock variability. A further argument for at least a weak intrinsic field is the absence of evidence of downward ionospheric convection (scale height depression by solar-wind pressure) in the Martian dayside atmosphere such as that proposed by Bauer and Hartle (1974) to explain Mariner—10 observations of Venus.

ACKNOWLEDGMENTS

The author is grateful to R. A. Wolf, F. C. Michel, R. E. Daniell, Jr., and K. I. Gringauz for their pertinent comments and suggestions. This work was supported by the Atmospheric Sciences Division of the National Science Foundation, N.S.F. Grant DES74-19668.

REFERENCES

Alfvén, H. and C. G. Falthammar, 1973, Cosmical Electrodynamics, 2nd. ed, Oxford University Press, London, p. 64.

Bauer, S. J. and R. E. Hartle, 1974, "Venus Ionosphere: An Interpretation of Mariner 10 Observations," Geophys. Res. Lett., 1, p. 7.

Cloutier, P. A., M. B. McElroy, and F. C. Michel, 1969, "Modification of the Martian Ionosphere by the Solar Wind," J. Geophys. Res., 74, p. 6215.

Cloutier, P. A. and R. E. Daniell, Jr., 1973, "Ionospheric Currents Induced by Solar Wind Interaction with Planetary Atmosphere," Planet. Space Sci., 21, p. 463.

Cloutier, P. A., R. E. Daniell, Jr., and D. M. Butler, 1974, "Atmospheric Ion Wakes of Venus and Mars in the Solar Wind," Planet. Space Sci., 22, p. 967.

Dessler, A. J., 1968, "Ionizing Plasma Flux in the Martian Upper Atmosphere," The Atmosphere of Venus and Mars, Brandt, J. C. and M. B. McElroy, eds., Gordon and Breach, New York, p. 241.

Dolginov, Sh. Sh., Ye. G. Yeroshenko, and L. N. Zhuzgov, 1973, "Magnetic Field in the Very Close Neighborhood of Mars According to Data from Mars-2 and Mars-3 Spacecraft," J. Geophys. Res., 78, p. 4779.

Gringauz, K. I., V. V. Bezrukikh, M. I. Verigin, and A. P. Remizov, 1974, "On Electron and Ion Components of Plasma in the Antisolar Part of Near Martian Space," Report of Institute for Space Research, Academy of Sciences, USSR. See also 1975, Kossmicheskiye Issledovaniya, 13, p. 123.

Michel, F. C., 1971, "So1ar-Wind-Induced Mass Loss from Magnetic Field Free Planets," Planet. Space Sci., 19, p. 1580.

119

Rassbach, M. E., R. A. Wolf, and R. E, Daniell, Jr., 1974, "Convection in a Martian Magnetosphere," J. Geophys. Res., 79, p. 1125.

Spreiter, J. R., A. L. Summers, and A. Y. Alksne, 1966, "Hydromagnetic Flow Around the Magnetosphere," Planet. Space Sci., 14, p. 223.

Spreiter,J. R., A. Y. Alksne, and A. L. Summers, 1968, "External Aerodynamics of the Magnetosphere," Physics of the Magnetosphere, Caravillano, R. L., J. F. McClay, and H. R. Radoski, eds., Reidel, Dordrecht, Holland, p. 301.

Spreiter, J. R., A. L. Summers, and A. W. Rizzi, 1970, "Solar Wind Flow Past Nonmagnetic Planets-Venus and Mars," Planet. Space Sci., 18, p. 1281.

QUESTIONS

Cloutier/Galeev: The asymmetry of the ionopause which results from the difference in the drift of photoions across the ionopause in the cases of inward and outward interplanetary electric fields will be diminished by two effects:

1. The collective interaction of photoions and solar-wind ions could prevent the photoions' acceleration up to solar-wind velocity and they will not experience a complete cycloidal trajectory.
2. If the ionopause is diffuse, then the difference between the inward and outward electric field cases will be smaller.

Cloutier/Ness: I point out that the last figure in your talk (see figure 2(a) in Rassbach et al., 1974) is not a quantitative model but rather a schematic suggestion which does not bear a close relationship to the geometry of the observed conditions at Mars by the Mars-2, -3, and -5 spacecraft. That is, you indicate a very wide magnetosphere and tailward region which does not conform to the experimental observations of a much narrower tail region.

Cloutier/Vaisberg: Do you think azimuthal asymmetry of an obstacle necessarily leads to asymmetry of the bow shock, since an azimuthal component of the flow may develop due to the differences of an obstacle from a figure of rotation?

Cloutier: Yes, I think shock asymmetry will result from obstacle asymmetry.

---